
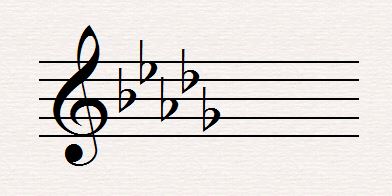
Seconds are probably the easiest intervals to identify. Major second, 2 half steps or one whole stepĪugmented second, 3 half steps or 1 1/2 whole steps Below you can see the number of half steps according to the quality of a second: Seconds can be major, minor, augmented or diminished. Please refer to each interval for more information. This is the reason why we need to specify the quality of an interval. For example the third D-F has 1½ whole steps or 3 half steps while C-E has 2 whole steps or 4 half steps: The same thing happens with other intervals. For example, the second between C and D has one whole step while the second between E and F has only one half step:

A black key, for example the one between C and D, can be considered a C sharp or a D flat:īy using the keyboard to count the number of half steps between notes we can see that intervals with the same numerical classification can contain a different number of half steps. They can be raised a half step with a sharp or lowered with a flat. These notes are considered natural notes. Notes corresponding to the white keys on the keyboard are called C, D, E, F, G, A and B.
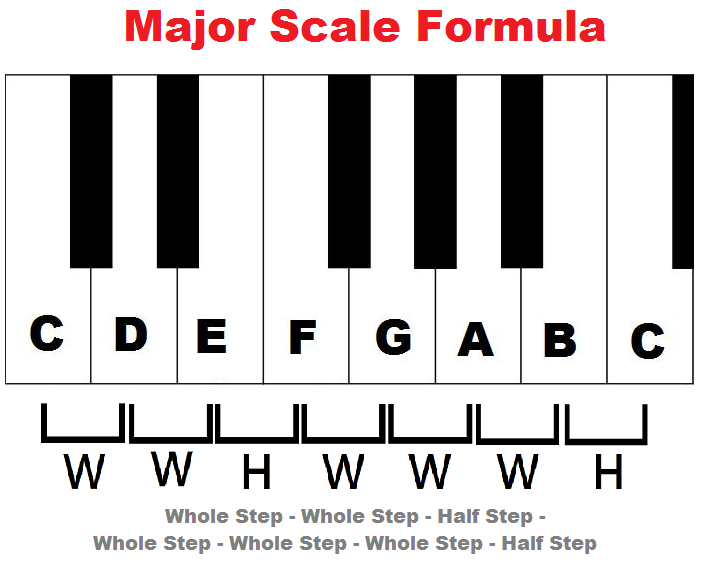
The keys that are not separated by a black key are at a distance of a half step: All the white keys on the keyboard separated by a black key are at a distance of a whole step. On the keyboard any key is at the distance of a half step from the next and previous key:Ī whole step contains two half steps. The distance between each note is known as a half step. In the equal temperament tuning system the octave is divided exactly in twelve notes. That is why we need to specify the quality by finding the exact number of whole and half steps in the interval. Yet, not all intervals of the same numerical classification are of the same size. In the next figure you can see the relationship between the number of notes and the numerical size of intervals: For example from C to E we have a third (C-1, D-2, E-3). To identify an interval we must know its numerical size and quality.īy counting the number of notes in an interval we obtain its numerical size. Enjoy!Īn interval measures the distance between two notes.


 0 kommentar(er)
0 kommentar(er)
